TransDEM Forum

Für vorbildnahen Streckenbau sind maßstäbliche Gleispläne hilfreiche Ressourcen. Siedelt man sein Streckenbauprojekt in den ersten Jahrzehnten der Bundesbahn an, so gilt das umso mehr, als die Infrastruktur im Zeichen der heutigen Plastikbahn doch massiv rückgebaut wurde. Aktuelle Karten oder Luftbilder können daher nur noch grobe Orientierung sein.

Nun sind maßstäbliche Gleispläne nicht unbedingt leicht zu bekommen. Eventuell findet man nur die verzerrte Variante, abgekürzt IVLZ. Diese Pläne weisen üblicherweise einen Maßstab von 1:1000 in der Längsachse auf, sind aber in der Querachse 1:3000 gestaucht.

Mit TransDEM ließen sich diese Pläne bislang nur dann nutzen, wenn die Längsachse in einer Geraden lag. Sobald die abgebildete Trasse Bögen aufweist, wurde es schwierig bis unmöglich, diese Pläne zu georeferenzieren. Das soll sich künftig ändern.

Schon von Anfang an bot TransDEM Funktionen, um digitale Höhendaten zu bearbeiten. Der wesentliche Ansatz dabei war die Verwendung eines Unregelmäßigen Dreiecksnetzes, englisch Irregular Triangular Network, abgekürzt TIN.

Ich habe nun versucht, den TIN-Algorithmus auf die Georeferenzierung zu übertragen. Eine der von TransDEM unterstützen Methoden bei der Eingabe von Koordinaten ist das Verfahren mit 3+1 Punkten. Die ersten drei Punkte erhalten dabei je Punkt ein Geokoordinatenpaar. Daraus ergeben sich sechs Gleichungen mit sechs Unbekannten, ausreichend, um eine einfache affine Transformation aus Translation, Rotation, Skalierung und Scherung zu bestimmen. Diese drei Punkte bilden ein Dreieck.

Neu kommt jetzt dazu, dass man nicht länger auf ein einziges Dreieck beschränkt bleibt, sondern durch weitere Stützpunkte beliebig viele Dreiecke erzeugen kann, wobei jeder Stützpunkt seine eigenen Geokoordinaten bekommt.

Dieser TIN-Algorithmus scheint tatsächlich auch für verzerrte IVLZ-Gleispläne anwendbar. Allerdings ist trotzdem viel Mühe und Sorgfalt erforderlich, um brauchbare Ergebnisse zu erzielen.

Dazu folgendes Beispiel:

Gegeben sei einer dieser üblichen verzerrten Pläne. Man beginnt damit, identifizierbare Punkte und deren Koordinaten zu finden, die man auf Luftbildern oder vielleicht der Deutschen Grundkarte entdeckt. In diesem Beispiel waren es zwei Weichenspitzen und ein Wasserdurchlass. Hierfür setzt man Punkte, wie bei der bisherigen Georeferenzierung, nur dass die in der TIN-Variante als Stützpunkte eines Dreiecksnetzes fungieren.

Das Wesen einen solchen Stützpunktes ist, dass seine Lage in Pixelkoordinaten bestimmt wird, er als Eigenschaft aber die zugehörigen Geokoordinaten zugewiesen bekommt. Durch die Triangulierung entstehen Dreiecke, und die drei Stützpunkte eines jeden Dreiecks bestimmen eine affine Transformation.

Jeder neue Stützpunkt bekommt automatisch einen Vorschlagswert für seine Geokoordinaten, der sich einfach aus dem Dreieck und seiner Transformation ergibt, in welchem der Mauszeiger sich gerade befindet. Auch das ist vergleichbar zur bisherigen Georeferenzierung.



Oft ist die Anzahl identifizierbarer Punkte sehr klein. Dann kann man eine Hilfsfunktion nutzen, wozu man einen der Stützpunkte als Referenzpunkt markiert und von dort Abstand und Richtungswinkel festlegen kann, z.B. entlang der Hektometermarken auf dem Plan. Angezeigte Richtung und Abstand sind dabei Geokoordinaten, nicht Pixelkoordinaten. Den wahren Richtungswinkel kann man in einer zweiten TransDEM-Instanz über Luftbild etc. ermitteln.



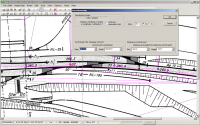
Ein Abstecken der Trasse auf diese Weise wird allein nicht ausreichen. Bedingt durch die Art der Triangulierung (Delaunay/Bourke) werden Dreiecke entstehen, die entweder fast keine Fläche aufweisen oder so ungünstig liegen, dass die Stützpunkte eine unsinnige Transformation ergeben. Abhilfe kann hier eine Verbreiterung des georeferenzierten Trassenbandes schaffen. Auch hierzu gibt es eine Hilfsfunktion. Markiert man drei Stützpunkte, so kann man TransDEM anweisen, für die durch die drei Punkte definierten zwei Strecken die Winkelhalbierende zu bilden und auf dieser zwei neue Stützpunkte anzulegen, im Abstand der ersten Strecke, zwischen erstem und zweiten Punkt, diesmal in Pixelkoordinaten. Der zweite Punkt wird danach automatisch als neuer Referenzpunkt markiert.





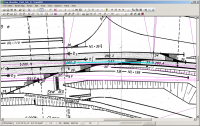
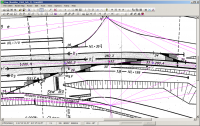
Hat man nun z.B. als erste Strecke eine Länge von 100 m und weiß man, dass der Plan lateral 1:3 verzerrt ist, so trägt man als Abstand dieser neuen Punkte auf der Winkelhalbierenden nicht 100m, sondern 33m ein. Das führt man für den ganzen Plan fort, wobei es sinnvoll ist, auch zwischendurch schon mal ein Ergebnis berechnen zu lassen (was auf langsamen Rechnern leider dauert), um Fehler frühzeitig zu entdecken.

Nach Abschluss der Stützpunktvorgabe könnte es so aussehen:



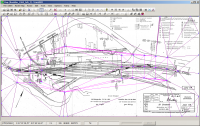
Transformiert ergibt sich dann folgendes Bild:



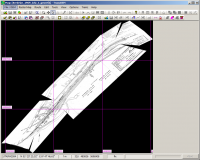
Die sichtbaren Einschnitte sind Folgen von Randreiecken, deren Stützpunkte der Algorithmus automatisch vergibt, die aber unzureichend bestimmt sein können. Um deren Einfluss klein zu halten, sollte das Georeferenzierungsband genügend breit gewählt werden, s.o.

Anschließend kann und sollte man den Plan noch sinnvoll beschneiden (eingebaute Funktion):



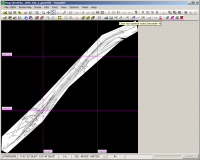
Zum Schluss die Gegenprüfung mit einer anderen georeferenzierten Datenquelle:



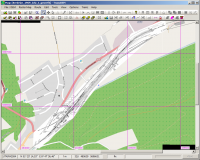
In diesem Beispiel wurden nur die eingangs gezeigten drei Stützpunkte mit individuell ermittelten Geokoordinaten versehen. Alle anderen Stützpunkte wurden abgeleitet. Dabei spielten die Hektometermarkierungen auf dem Plan eine wesentliche Rolle. Wahre Winkel wurden in einem zweiten TransDEM-Fenster bestimmt oder geschätzt. War es bei der Längsabsteckung nicht ganz aufgegangen, wurden die Fehler Pi mal Daumen verteilt.

Das Verfahren mit TIN funktioniert also, bleibt aber immer noch recht aufwändig und fehlerträchtig, vor allem deswegen, weil man nicht sofort die visuelle Kontrolle bekommen kann. Es soll auch nicht als Ablösung der simpleren 3+1-Punkte-Georeferenzierung gesehen werden, sondern nur dann angewendet werden, wenn das einfachere Verfahren keine akzeptable Lösung ergibt. Ohne die beiden Hilfsfunktionen Abstand/Richtung und Winkelhalbierende habe ich mit TIN für die Gleispläne allerdings keinen Erfolg erzielen können.

An andere Stelle hatte ich schon erwähnt, die Geotransformation im TIN-Verfahren ist der rechenaufwändigste Algorithmus, den TransDEM bisher zu bewerkstelligen hatte. Ich lasse, soweit möglich, die Rechenschleifen parallel laufen, so dass bei einem Mehrkernrechner alle Kerne effizient genutzt werden.